Solving the Lost YubiKey problem with WebAuthn PRF & Shamir Secret Sharing.

Standard account recovery relies on centralized servers or passwords. While FIDO Alliance recommends registering multiple authenticators as backup, this approach proves impractical and costly for average users. Consequently, many services implement fallback authentication methods (passwords, SMS codes), creating a critical vulnerability: downgrade attacks. Attackers exploit these weaker recovery mechanisms through social engineering, with research showing 55 % of users falling for real-time phishing and 35 % vulnerable to FIDO downgrades^{[bicakci2022]}—effectively reducing account security to its weakest link.

Shamir’s Secret Sharing (SSS) offers a decentralized alternative. Unlike standard backups that simply copy data, SSS splits a passkey’s private key into multiple unique parts called shares. This method allows for secure recovery without a single point of failure or reliance on weaker authentication methods.

Practical Implementation Architecture

Since the WebAuthn SSS extension does not currently exist in the standard, we propose a browser extension-based approach that achieves the same security goals. This system functions as a modern, passwordless identity manager with account recovery capabilities in case of hardware key loss.

System Components

Master Key (MK): A random key generated within the extension. This is the root secret that encrypts all user data (website passwords, notes, etc.).

YubiKey (Authenticator): Used to unlock the MK during normal operation via WebAuthn PRF extension.

SSS (Shamir Secret Sharing): Enables MK recovery during catastrophic failure (YubiKey loss).

Browser Extension: The orchestration layer. Performs encryption, communicates with the authenticator, and isolates the process from web pages.

Phase A: Registration (Identity Creation)

The registration phase securely creates the Master Key, encrypts it, and establishes backup mechanisms:

1. Generation: The extension generates a cryptographically strong random Master Key (MK) in memory.

2. WebAuthn PRF: The extension prompts the user to insert their YubiKey and calls navigator.credentials.create with the prf extension enabled.

   • A random salt is transmitted to the authenticator.
   • The YubiKey returns a PRF output (deterministic key bound to the hardware).

3. Encryption: The extension uses the PRF output as a key-encryption key (KEK) and encrypts the Master Key, producing Encrypted_MK.

4. Backup (SSS): The extension takes the Master Key (unencrypted) and mathematically splits it into $n$ shares using SSS with threshold $k$ (e.g., 2-of-3):

   • Shares are distributed across independent storage locations to prevent single points of failure
   • Examples include: remote servers, physical media (QR codes, printed backups), hardware authenticator storage (largeBlob), or trusted contacts
   • The distribution strategy balances availability (easy recovery) with security (preventing unauthorized reconstruction)

5. Cleanup: The extension securely erases both MK and PRF output from RAM.

Phase B: Normal Login

Normal authentication quickly unlocks the vault using the hardware authenticator:

1. Initiation: User arrives at their device with the extension locked.

2. Data Retrieval: Extension downloads Encrypted_MK and salt from the server.

3. Key Derivation: Extension calls navigator.credentials.get with the stored salt.

   • User touches their YubiKey.
   • YubiKey internally computes and returns the same PRF output as during registration.

4. Decryption: Extension uses the PRF output to decrypt Encrypted_MK.

5. Result: Extension has the Master Key in memory. User is authenticated and the extension can autofill passwords or generate passkeys.

Phase C: Recovery

Recovery enables account access when the user loses their YubiKey:

Critical constraint: Without the YubiKey, obtaining the PRF output is impossible, rendering Encrypted_MK stored on the server cryptographically useless.

1. Initiation: User on a new device (or with a new authenticator) clicks “Recover Account” in the extension.

2. Share Collection: Extension collects at least $k$ shares from their distributed storage locations:

   • Remote shares may require authentication (e.g., email verification, OAuth)
   • Physical shares require user input (scanning QR codes, entering text)
   • The specific retrieval mechanism depends on the storage medium chosen during registration

3. Reconstruction: Extension mathematically combines the shares. If valid, the polynomial evaluation yields the original Master Key.

4. Key Rotation (Re-encryption):

   • User is now authenticated.
   • Extension prompts: “Insert NEW YubiKey”.
   • Repeats Phase A process (obtaining new PRF output from new authenticator and re-encrypting the Master Key).
   • Old Encrypted_MK on server is replaced with the new version.

Security Properties

Zero-Knowledge Server: The server observes only an encrypted blob, salt, and optionally one SSS share. None of these components provide useful information without the remaining elements.

Phishing Protection: Normal authentication requires physical possession of the hardware authenticator.

Loss Protection: Hardware loss does not result in loss of digital identity (thanks to SSS).

Isolation: Browser extensions execute in an isolated context separate from web page main-world scripts^{[mdn_content_scripts][mdn_executionworld]}. This architectural boundary prevents malicious JavaScript on compromised websites from accessing the extension’s memory space or the Master Key, even if the visited page contains XSS vulnerabilities.

Mathematical Foundation

The core of this scheme relies on polynomial interpolation. The fundamental idea is that it takes $k$ points to uniquely define a polynomial of degree $k-1$.

To protect a secret $S$, we construct a random polynomial $q(x) \in \mathbb{Z}_p[x]$ of degree $k-1$ where $q(0) = S$. The polynomial is defined as:

$$q(x) = S + a_1 x + a_2 x^2 + \dots + a_{k-1} x^{k-1} \pmod{p}$$

In this equation:

• $S$ represents the secret key material
• $p$ is a cryptographically large prime satisfying $p > \max(S, n)$
• Coefficients $a_1, \dots, a_{k-1} \in \mathbb{Z}_p$ are chosen randomly from a uniform distribution
• All arithmetic operations are performed in the finite field $\mathbb{Z}_p$

The share generation evaluates $q(x)$ at $n$ distinct non-zero points to produce shares $(i, q(i))$ for $i \in \{1, \dots, n\}$.

Secret reconstruction requires collecting at least $k$ shares. Given these points, we apply Lagrange interpolation^{[burden2011, p. 108]} to calculate $q(0)$ and retrieve the private key^[shamir1979].

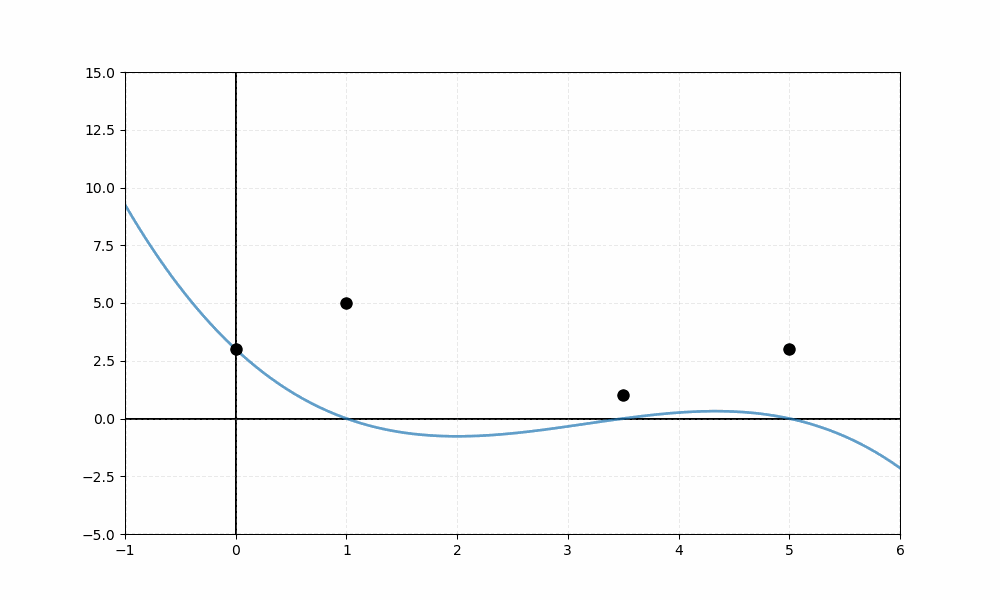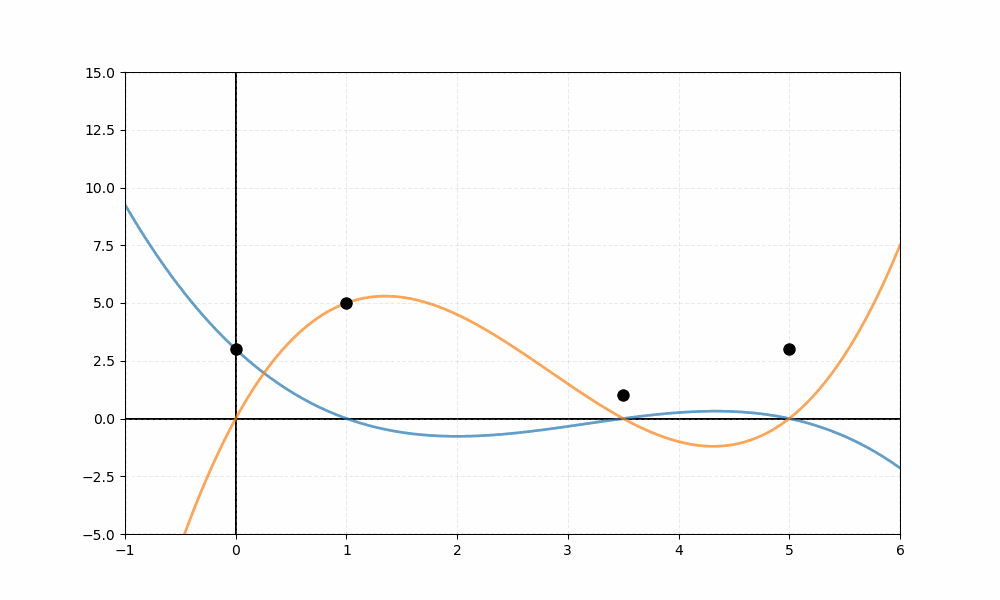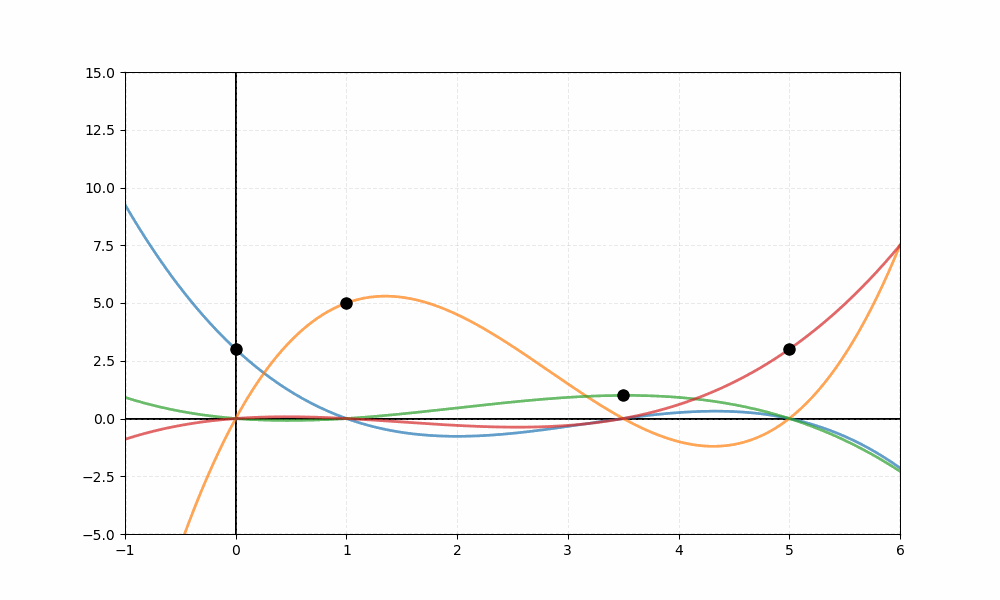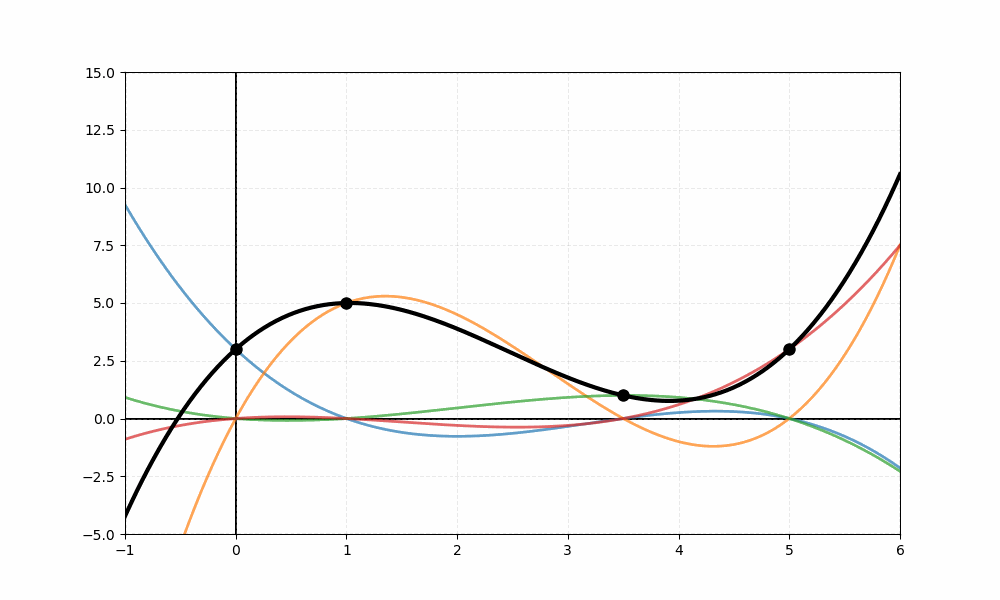Figure 1: Lagrange interpolation reconstructing a polynomial from threshold shares. The animation demonstrates how $k$ points uniquely determine a polynomial of degree $k-1$, enabling secret recovery.

The visualization depicts four data points $(0, 3), (1, 5), (3.5, 1), (5, 3)$ represented as black dots. The animation sequentially reveals four colored curves—each a Lagrange basis function $L_i(x)$ weighted by its corresponding $y_i$ value, where the basis polynomial is generally defined as:

$$L_i(x) = \prod_{\substack{j=0 \\ j \neq i}}^{k-1} \frac{x - x_j}{x_i - x_j}$$

For these specific points, the four basis functions are:

$$L_0(x) = \frac{(x-1)(x-3.5)(x-5)}{(0-1)(0-3.5)(0-5)}, \quad L_1(x) = \frac{(x-0)(x-3.5)(x-5)}{(1-0)(1-3.5)(1-5)}$$ $$L_2(x) = \frac{(x-0)(x-1)(x-5)}{(3.5-0)(3.5-1)(3.5-5)}, \quad L_3(x) = \frac{(x-0)(x-1)(x-3.5)}{(5-0)(5-1)(5-3.5)}$$

The blue curve represents $y_0 \cdot L_0(x) = 3 \cdot L_0(x)$, orange shows $y_1 \cdot L_1(x) = 5 \cdot L_1(x)$, green displays $y_2 \cdot L_2(x) = 1 \cdot L_2(x)$, and red illustrates $y_3 \cdot L_3(x) = 3 \cdot L_3(x)$. In the final frame, the thick black line represents the reconstructed polynomial $q(x) = 3 \cdot L_0(x) + 5 \cdot L_1(x) + 1 \cdot L_2(x) + 3 \cdot L_3(x)$—the sum of all four weighted basis functions—which passes exactly through each of the four data points.